С6:
На доске в порядке возрастания написаны пять различных натуральных чисел. Известно, что если стереть первое или последнее из них, то сумма любых двух оставшихся чисел будет больше любого другого из оставшихся чисел.
a) Может ли пятое число быть в 100 раз больше, чем первое?
b) Может ли пятое число в 3 раза больше, чем второе?
c) Какое наибольшее значение может принимать отношение суммы первого и пятого чисел к сумме второго и четвёртого, если третье число равно 100?
Решение:
a) Пусть это числа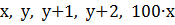 
. По условию задачи 
При 
.
Тогда условию задачи удовлетворяют числа 3,150,151,152,300.
b) Пусть это числа 
. По условию задачи 
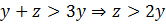, но по условию задачи 
– противоречие. Значит, пятое число не может быть в три раза больше второго.
c) Будем искать числа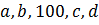 
в виде 
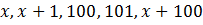– из соображений, что 
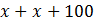– должно быть как можно больше(чем меньше разность между числами a и b, тем a- больше ), 
- как можно меньше(чем меньше разность между числами 100 и c, тем c - меньше ), кроме этого должно выполняться условие b+100>d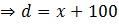 
.
Найдём, при каком значении x отношение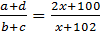 
будет наибольшим.
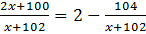– тем больше, чем больше 
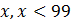. Тогда при 
получим числа:
. Тогда наибольшее отношение 
