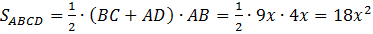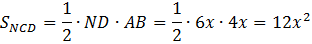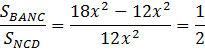С4:
В трапецию ABCD с основаниями AD>BC можно вписать окружность. Биссектрисы углов при вершинах B и C пересекают основание AD в точках M и N соответственно.
a) Докажите, что площадь четырёхугольника ABCN равна площади треугольника ABM
b) Точка касания окружности, вписанной в трапецию ABCD, делит её основание в отношении 2:1, считая от вершины B, угол 
. В каком отношении прямая CN делит площадь трапеции?
Решение:
Для того, чтобы доказать утверждение а) достаточно доказать равновеликость треугольников BOC и MON, где O – центр окружности вписанной в трапецию(точка пересечения биссектрис). Так как центр вписанной окружности равноудалён от оснований трапеции, то высоты подобных треугольников BOC и MON равны, соответственно и сами треугольники равны между собой. Получили, что треугольники BOC и MON равновелики, значит, площадь четырёхугольника ABCN равна площади треугольника ABM.
Биссектрисы, проведённые из вершин боковой стороны трапеции, пересекаются под прямым углом. Кроме этого треугольники CEO и OED подобны: 
;
Тогда 
