Задумано несколько целых чисел. Набор этих чисел и все их возможные суммы (по 2 по 3 и т.д.) выписывают на доску в порядке неубывания. Например, если задуманы числа 2,3,5 то на доске будут выписаны числа 2,3,5,7,8,10
а) На доске выписан набор -13,-8,-6,-5,-1,2,7 Какие числа были задуманы?
б) Для некоторых различных задуманных чисел в наборе написанном на доске 0 встречается ровно 7 раз. Какое наименьшее количество чисел могло быть задумано?
в)Для некоторых задуманных чисел на доске выписан набор. Всегда ли по этому набору однозначно можно определить задуманные числа?
Решение:
а) Всего различных непустых множеств из n-элементов множества можно составить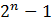 
. На доске выписано 7 чисел, значит они составлены из трёх чисел. Среди этих чисел есть как положительные, так и отрицательные. Если задумано число 2, а число 7 нет, то оно составлено из нескольких двоек, однако числа 2+2=4 нет на доске. Тогда 7 – задумано, но числа 7+2=9 нет на доске. Значит из положительных чисел задумано только 7. Из отрицательных чисел задуманы два. Числа -6,-1 задуманы быть не могут, так как 7-6=1;7-1=6. Число -13 не задумано, так как в сумме с любым из других отрицательных чисел даёт числа меньшие, чем записанные на доске. Итак, задуманными числами могут быть только -8,-5,3.
б) Для четырёх и трёх различных чисел максимальное количество нулей на доске -3, для двух –один нуль. Если было задумано 5 чисел, то 7 нулей можно получить если одно из них нуль, а четыре других образуют две пары противоположных по знаку чисел:
0,a,-a, b,-b. (0);(a-a);(b-b);(0+a-a);(0+b-b);(a-a+b-b);(0+a-a+b-b) -7сумм. Ответ n=5.
в) Нет не всегда. Так два различных набора задуманных чисел
a,b,(-a-b) и –a,-b,(a+b) дают одинаковый набор на доске a,b,-a,-b,a+b,-a-b,0.
