С2:
В треугольной пирамиде MABC основанием является правильный треугольник ABC ,ребро MB перпендикулярно плоскости основания, стороны основания равны 3, а ребро MA равно 6. На ребре AC находится точка D, на ребре AB находится точка E, а на ребре AM – точка L. Известно, что AD=2 и BE=ML=1. Найдите угол между плоскостью основания и плоскостью, проходящей через точки E,D и L.
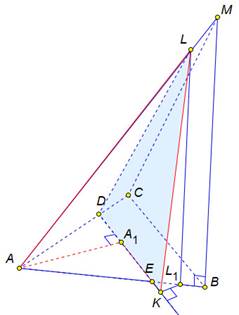Воспользуемся теоремой косинусов для двугранного угла A(A1K)L:
AL=5; 
;
Тогда угол между плоскостями (ABC) и (EDL) равен 
Ошибки:
1) В ответе – тупой угол.
2) LK=LE
