8.1 Найдите все пары целых чисел (x;y), удовлетворяющих уравнению 
.
8.2 Дан угол AOB (A и B-точки а сторонах угла). Как построить прямую
, проходящую через вершину O так, чтобы площади треугольников AOC и BOD, где C и D – основания перпендикуляров, опущенных из точек A и B на прямую , были равны?
8.3 Шесть точек расположены на плоскости так, что все попарные расстояния между ними не больше 1. Докажите, что из них можно выбрать три точки, попарные расстояния между которыми строго меньше 1.
8.4 Сколько существует целых значений параметра a, при которых уравнение 
имеет два корня разных знаков?
8.5 В сосуде было 20 литров чистого спирта. Часть этого спирта отлили, а сосуд долили водой. Затем отлили столько же литров смеси и сосуд опять долили водой. После этого в сосуде оказалось чистого спирта втрое меньше, чем воды. Сколько литров спирта отлили в первый раз?
------------------------------------------------------------------------------------------------------------------------------------------
9.1 Дана сетка(сторона клетки –одна верёвочка) :
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
Сколько верёвочек максимально можно перерезать, чтобы сетка не распалась на части, если n=2015?
9.2 Докажите, что 
делится на 133 для любого натурального n.
9.3 Найдите положительные решения уравнения 
9.4 Докажите ложность или истинность высказывания 
9.5 В треугольнике ABC точка K делит сторону BC в отношении 1:2, считая от точки B; точка H делит сторону AC в отношении 2:3 , считая от точки A; отрезки BH и AK пересекаются в точке M. Найдите отношение площадей треугольников BMK и AMH.
10.1 На доску выписали по порядку все натуральные числа от 1 до 2014. Затем стёрли все цифры кроме нулей и единиц. Сколько всего выписано нулей? Сколько выписано единиц? Сколько всего двоичных чисел можно составить из всех этих нулей и единиц?
10.2 Алфавит некоторого племени содержит 4 буквы – две гласные и две согласные. Каждое слово языка этого племени состоит не более чем из десяти букв. Сколько всего различных слов может содержать этот язык? Какой процент слов, состоящих только из гласных букв?
10.3 Докажите равенство 
10.4 Найти все значения параметра a, при каждом из которых неравенство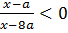 
выполняется для всех 
таких, что 
10.5 Площадь треугольника ABC равна P. Прямая DE, параллельная основанию AC, отсекает от треугольника ABC треугольник BDE, площадь которого равна Q. На стороне AC взята произвольная точка M и соединена отрезками прямых с точками D и E. Чему равна площадь четырёхугольника BDME?
________________________________________________________________________________
11.1 Решить уравнение 
11.2 Найдите все значения m, при которых система имеет единственное решение 
11.3 Существует ли такая арифметическая прогрессия, в которой сумма любого числа её членов равна а) квадрату числа членов б) кубу числа членов
11.4 В выпуклом четырёхугольнике ABCD отрезки, соединяющие середины противоположных сторон, пересекаются под углом 60⁰, а их длины относятся как 1:3. Чему равна меньшая диагональ четырёхугольника ABCD, если большая равна 
?
11.5 Найдите ГМТ равноудалённых от начала координат и прямой, проходящей через точки с координатами (3;0); (0;-4)
